深度学习课程笔记

本文来自于李宏毅老师的深度学习课程

《MACHINE LEARNING 2023 SPRING》

监督式学习

将数据分为输入与输出两类，让机器寻找其中的联系，即 $f (x) = y$ ,找出f()这个func，这种模式受限于数据的容量大小。

预训练（自监督式学习）

通过某种方法成对产生输入输出数据（比如diffusion的噪声），并进行训练，这便是 自监督学习 。而使用此类方法生成的模型又被称为基石模型（底模），一般我们会将预训练的模型再次进行监督式学习。

增强式学习（强化学习）

同样的输出内容，由人类判断好坏（浅层反馈 Shallow Learning），对机器的某个判断进行奖励（Reward）。

Neural Network

现如今，最受瞩目的 deep learning 方向则就是 Neural Network 。与其相关的两个新兴问题：Neural Editing与Neural Unlearning。

Deep Learning Step

define a set of Function (Neural Network)
Goodness of Function
pick the best Function

Neural 形如下图：

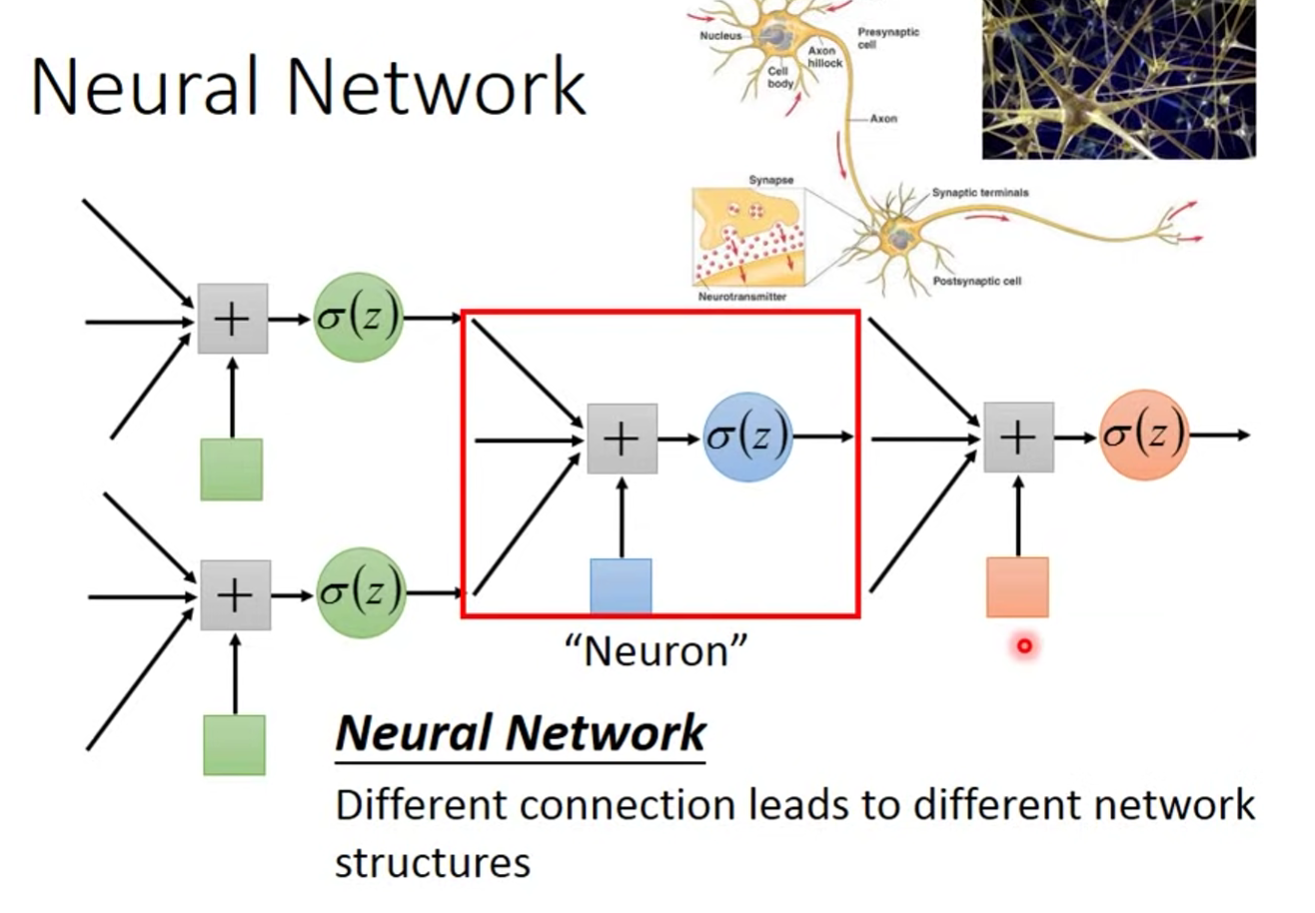
如果我们以不同的方式去链接 Neural ，就可以得到不同的 Structures. Different connection leads to different network structures.

Neural Network Parameter $θ$ : all the wight and biases in the "network"

Network Connect Way

Fully Connect Feedforward （全连接前馈网络）

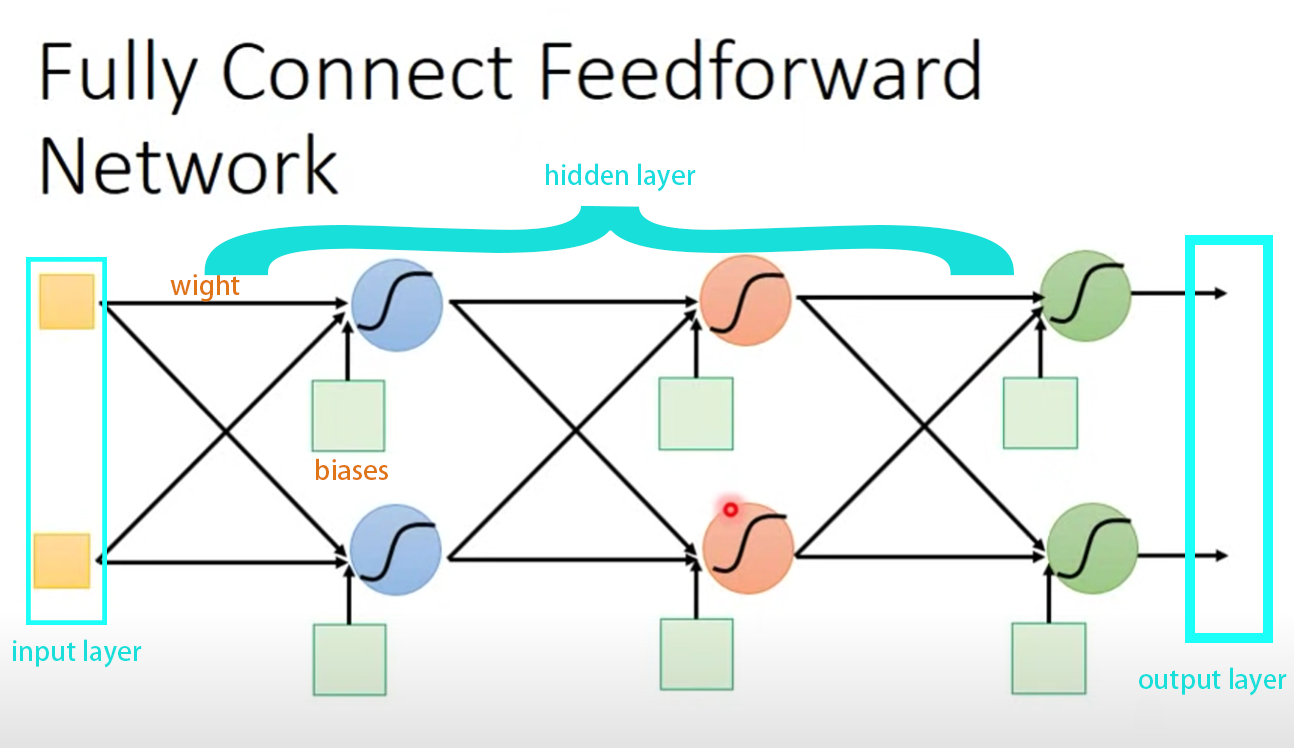
Input -> hidden layer/Feature extractor replacing/Softmax function -> output = muti-class Classifier

wight 和 biases 是通过train data去寻找的。

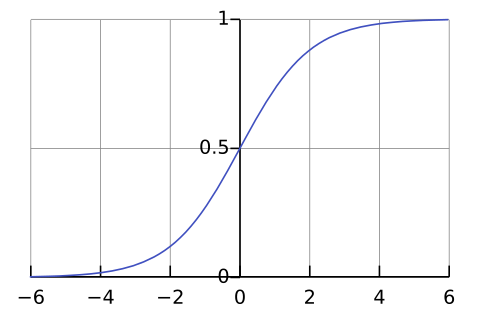
Sigmoid Function: $σ (z) = \frac{1}{1 + e ^{-} z}$

$z = w * x + b$ ，随后丢入 Sigmoid function，就得到一个probability，它被用于 Logistic Regression （逻辑回归），将变量映射到 $(0, 1)$ 中。

当仅决定了 structure 而没有 wight 和 biases 的时候，则称为 define a function set 。 Network 就是一连串的 Matrix 运算。

Deep = Many hidden layer

一般来说，hidden layer越多，训练出来的效果越好。

当设计完成 structure 即一个 function set ，不同的 wight 和 biases 对应不同的 function 。

找到 Network Structure 仅能凭借经验与直觉。

Total Loss

对于每一个 input data ，我们还有与之相对应的 target data ，一般来说我们会计算每一个 output 与 target 之间的 Cross Entropy 让这个数值越小越好。

$C (y, \overset{y}{^}) = - \sum_{i = 0}^{n} \overset{y_{i}}{^} ln y_{i}$

而将所有 output data 与 target 的 C 相加，就得到了 Total Loss 。

$L = \sum_{n = 0}^{N} C^{n}$

Find a function in function set that minimizes total loss L .

Any continuous function $f = R^{n} \to R^{m}$ can be realized by a network with one hidden layer.

Gradient Descent (梯度下降)

Gradient : Loss 的等高线方向。

Network parameter $θ = {w_{1}, w_{2} ... b_{1}, b_{2} ...}$

In step 3,we have to solve the following optimization problem: $θ^{*} = a r g min L (θ)$

θ^{0} \Rightarrow C o m p u t e \nabla L (θ^{0}) \Rightarrow [\partial L (θ^{0}) / \partial w^{1} \partial L (θ^{0}) / \partial w^{2} ⋮ \partial L (θ^{0}) / \partial b^{1} \partial L (θ^{0}) / \partial b^{2}] \Rightarrow θ^{0} - η \nabla L (θ^{0}) = θ^{1}

$η$ 则指 Learning Rate ，通过设置不同大小的 learning rate ，让函数更新 wight 和 biases ，达到最小 Loss

θ^{i} = θ^{i - 1} - η \nabla C (θ^{i - 1})

Adaptive Learning Rate

Learning Rate 应该随着训练次数而减小，如 decay: $η^{t} = \frac{η}{t + 1}$ 但最好还是给每一个不同的 parameter 一个不同的 learning rate 。

Vanilla Gradient Descent

$w^{t + 1} \leftarrow w^{t} - η^{t} g^{t}$

w is one wight

Adagrad

Divide the learning rate of each parameter by the root mean square of its previous derivatives.

将个学习率都除以之前算出来的微分的RMS（均方根差），RMS实际上是在模拟w的二次微分

$w^{t + 1} \leftarrow w^{t} - \frac{η ^{t}}{σ ^{t}} g^{t}$

g是偏微分的值， $σ^{t}$ 是过去所有微分值的RMS：

$σ^{t} = \frac{1}{t + 1} \sum_{i = 0}^{t} (g^{i})^{2}$

$η^{t} = \frac{η}{t + 1}$

Stochastic Gradient Descent

寻常的，我们取Loss通常会计算所有 training sample，然而Stochastic Gradient Descent只选择一个 example $x^{n}$

Feature Scaling

Make different features have the same scaling.

将不同的 features 设置在一个相同的scaling范围中。

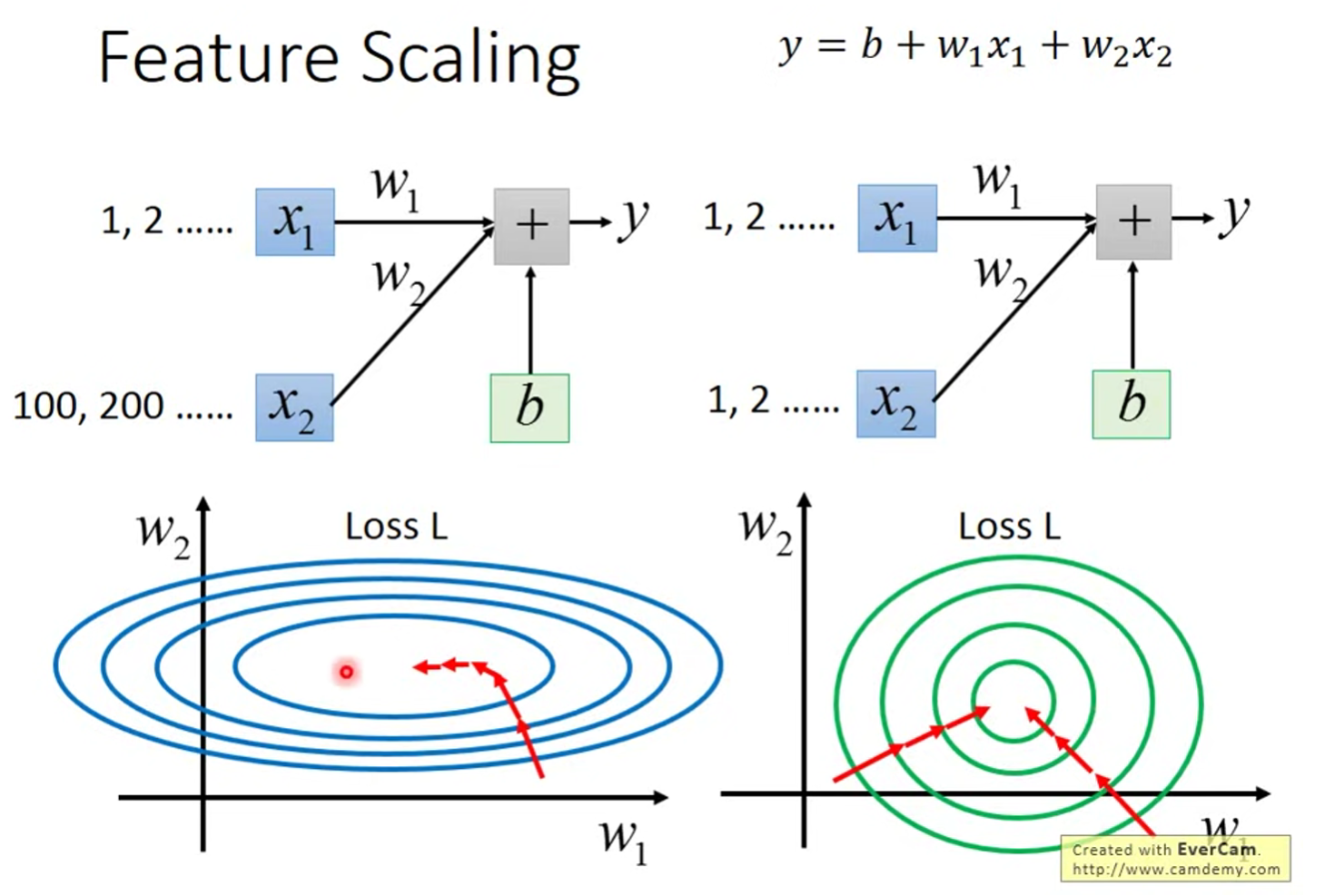
Feature Scaling

如 Error Surface 所示，相对于差异较大的x，差异较小的在GD的时候更容易接近最低点。

Back propagation

To computed the gradient decent efficiently, we use backpropagation.

Chain Rule

Rule: $g (x) = y$ ; $z = h (y)$

$Δ x \to Δ y \to Δ z \Rightarrow \frac{d y}{d x} = \frac{d z}{d y} \frac{d y}{d x}$

Loss function: $L (θ) = \sum_{n = 1}^{w} C^{n} (θ)$

其中, $C^{n}$ 即指输出 $y^{n}$ 与 Expert $\overset{y}{^}^{n}$ 之间的distance function.

则w对Total Loss的偏微分则为: $\frac{\partial L ( θ )}{\partial w} = \sum_{n = 1}^{N} \frac{\partial C ^{n} ( θ )}{\partial w}$

Regression 回归

$x^{1}$ 上标代表编号

$x_{1}$ 下标代表feature

Step 1: Model

A set of function.

$y = w * x + b$ (linear function)

$y = \sum w_{i} x_{i} + b$

Step 2: Goodness of function

设有Data组 $(x^{1}, \overset{y}{^}^{1}) \dots (x^{10}, \overset{y}{^}^{10})$ ，由此推断 function set ，需判断 function set 好坏。

定义一个 Loss function L :

L(a function of function set) => how bad it is

$L (f) = L (w * x + b) = \sum_{n = 1}^{10} (\overset{y}{^} - (b + w * x^{n}))^{2}$

(这里为啥要用2次方)

Step 3: Gradient Descent

$w^{*} = a r g min L (w)$

pick a random $w^{0}$ value
compute $\frac{d L}{d w} ∣_{w} = w^{0} \Rightarrow w^{1} \leftarrow w^{0} - η \frac{d L}{d w} ∣_{w = w^{0}}$

但存在 local optimal 而非 global optimal 的问题。

\nabla L = [\partial L / \partial w \partial L / \partial b]_{G r a d i e n t}

OverFitting (过拟合)：在不断选择复杂Model的同时，Loss在训练集上下降，而在测试集上提升。

L = Σ_{n} (\overset{y}{^}^{n} - (b + Σ w_{i} x_{i}))^{2} + λ Σ (w_{i})^{2}

Classification 分类

$x \to f u n c t i o n \to Cl a ss N$

Q:为什么不能以Regression的方式做Classification？

A:若样本偏差过大，function会偏向一边来寻求最小的方差。因此Regression good function的定义在Classification不适用。

Ideal Alternative

function(Model): $x \to {g (x) e l se Class 1 Class 2$
Loss function : $L (f) = \sum_{n} δ (f (x^{n}) \neq = \overset{y}{^}^{n})$
find best function : Perceptron,SVM

Gaussian distribution

f_{μ Σ} (x) = \frac{1}{2 π ^{\frac{1}{2}}} \frac{1}{∣Σ∣} e x p {- \frac{1}{2} (\frac{x - μ}{Σ})^{2}}

mean $μ$

covriance matrix $Σ$

对每一个Sample进行Maximum likelihood 极大似然值估计计算，可得出： $L (μ, Σ) = f_{μ Σ} (x^{1}) \dots f_{μ Σ} (x^{n})$ ，即可能性最大的Function

$(μ^{*}, Σ^{*}) = a r g ma xL (μ, Σ)$

多个class的时候，将多个Gaussian分布的 $Σ$ 定为同一个Matrix，即 $L (μ_{1}, μ_{2}, \dots μ_{n}, Σ) = f_{μ_{1}, Σ} (x^{1}) \dots f_{μ_{1}, Σ} (x^{n}) f_{μ_{2}, Σ} (x^{n + 1}) \dots$

当 $μ_{1} = μ_{2}$ 时，L最大。 $Σ = \frac{n}{n + m} Σ_{1} + \frac{m}{n + m} Σ_{2}$

机率模型的选择：经验与直觉

Gaussian：feature之间存在内在联系，而非independence。

Logistic Regression

	Logistic	linear
Step 1	$f_{w b} (x) = σ (\sum_{i} w_{i} x_{i} + b)$ out: between [0,1]	$f_{w b} (x) = \sum_{i} w_{i} x_{i} + b$ out: any value
Step 2	Traning Data: $(x^{n}, \overset{y}{^}^{n})$ $\overset{y}{^}^{n}$ :Classification $L (f) = \sum_{n} C (f (x^{n}), \overset{y}{^}^{n})$	Traning Data: $(x^{n}, \overset{y}{^}^{n})$ $\overset{y}{^}^{n}$ : Real number $L (f) = \frac{1}{2} Σ (f (x^{n}), \overset{y}{^}^{n})^{2}$
Step 3	$w_{i} \leftarrow w_{i} - η Σ_{n} - (\overset{y}{^}^{n} - f_{w, b} (x^{n})) x_{i}^{n}$	Like Left

Cross Entropy在Logistic Regress 上作为梯度下降的效率胜于Square Error。

Generative Model (生成模型)	Discriminative Model (识别模型)
受Data影响小	受Data影响大
有预先假设	neural network

Multi-class Classification

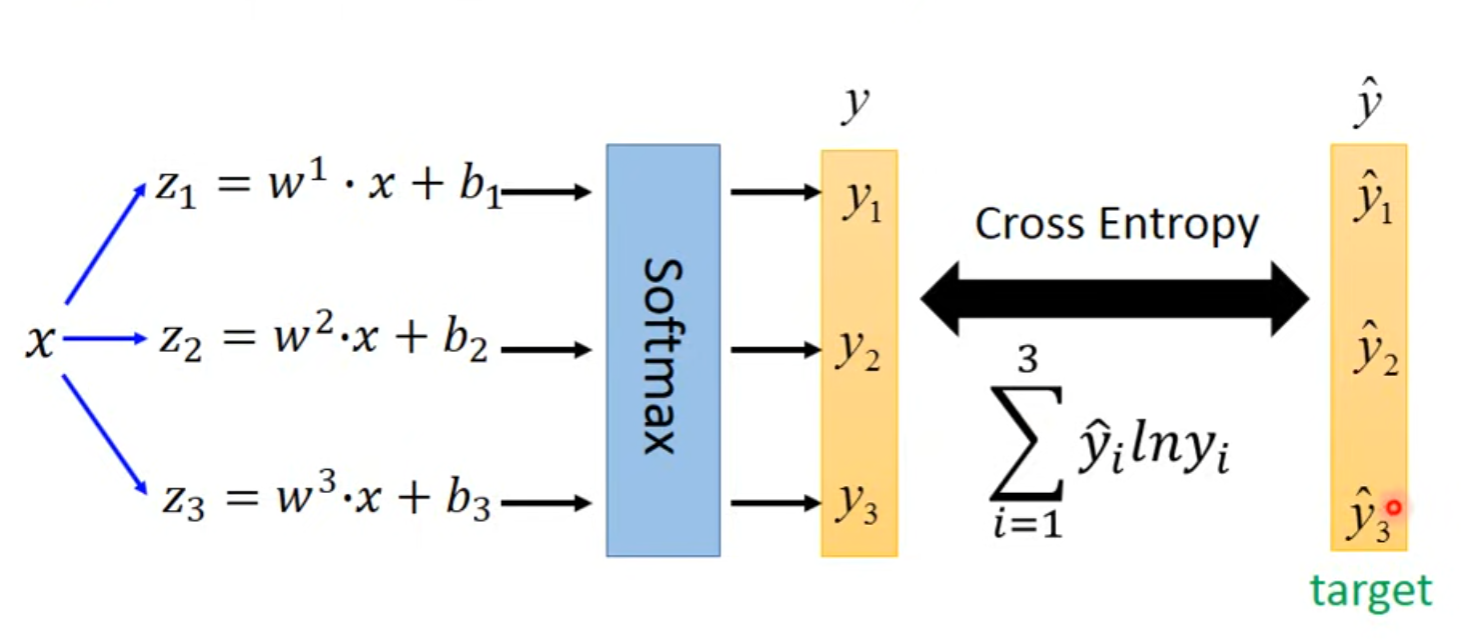
20230618204117304

$C_{1} = w^{1}, b^{1}$ $z_{1} = w^{1} x + b^{1}$

$C_{2} = w^{2}, b^{2}$ $z_{2} = w^{2} x + b^{2}$

$C_{3} = w^{3}, b^{3}$ $z_{3} = w^{3} x + b^{3}$

soft-max

$y_{i} = P (C_{i} ∣ x) \Rightarrow D (0, 1), \sum_{i} y_{i} = 1$

在 $y_{i}$ 与 $\overset{y}{^}^{i}$ 之间做cross entrpy， $- \sum_{i = 1}^{3} \overset{y}{^}_{i} ln y_{i}$ ，当Logistic Regression不断对feature进行变换，让model连结成Network，即是Neuro Network，这便是Deep Learning。

Network 架构设计

Convolution Neural Network (CNN)

在人类的观察中有这样的现象：某张图片如果含有数个特征符合某物，我们便认为此图片内含某物。CNN的思想与其如出一辙，它定义一个Receptive Field对图片进行特征提取。

Simplification Typical Setting

All Channels
Kernel Size - 3x3
Stride 2

Params Sharing即是在不同的 Neural 里使用相同的wight，从CNN的角度看，就是对不同区域进行特征提取。

Benefit of Convolution layer

在使用CNN之后，相比起Fully Connect Layer弹性变小了，而Params Sharing进一步降低了弹性，然而这并不是一件坏事，CNN在具有较高Model Bias的情况下Overfitting的可能性降低了。

另外一个故事

从另外一个角度来看CNN，每一个Filter对图片进行inner product，形成一个高维的Feature Map，在不断通过Convolution之后，图片会rescale。

Pooling - Max Pooling

通常来说，Convolution之后会接Pooling，即选定一个范围之后按照某种规则选择范围内最符合规则的Feature去代表这个范围。池化的目的是快速缩小图片、减少运算量。

$I m g \to C o n v o l u t i o n \to P oo l in g \to F u llC o nn ec t$

Self-attention

当Vector as Input，对于Input、Output大小长度不同，可分为三种类型。

N->N
N->one label
N->N'

自注意机制用于面向Seq2Seq，即Input、Output动态大小的情况。使用Self-attention对vector进行预处理，将Content的内容加权到本身的Vector上。Self-Attention对于某一个Vector，会注意它与content其他vector之间的相关性，如： $v_{1} w_{k} \cdot v_{2} w_{q} = α$ (dot-product),或 $t ec h (v_{1} w_{k} \cdot v_{2} w_{q}) W = α$ (additive)

注意:v1也会与自己计算相关性

如果将Self-attention的Input看作一个整体的矩阵,那便是: $O = K^{t} I w^{q}$

Multi-head Self-attention

different type of relevance，乘以不同的矩阵，得出结果再相加。

Position Encoding

self-attention无法标识将先后顺序与位置信息，就需要使用Position Encoding。

Self-attention	CNN
考虑全图	只考虑Filter
需要更多Data	只需要少量Data

CNN是一个Self-attention的特例，Self-attention则是考虑全图的CNN

Transform

transform是为了解决Seq2Seq问题的模型架构，而Seq2Seq可以用在各种问题上，作为一种通解。

$I n p u t \to E n co d in g \to Deco d in g \to O u tp u t$

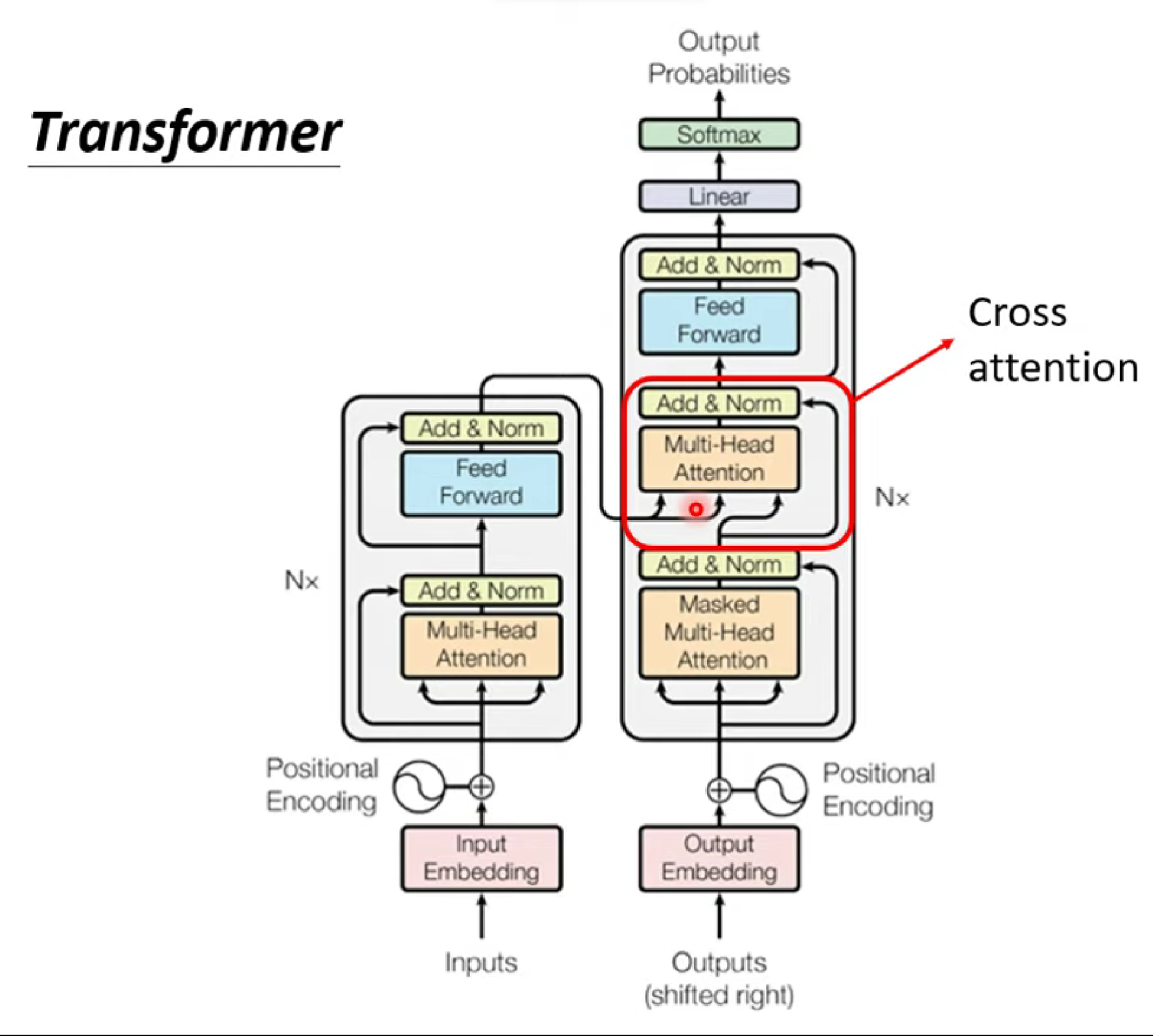
Encoder

Encoder是一个输入、输出同样长度向量的 Block ，在Transform中，Encoder就是Self-attention。

Residual Connection 残差链接

即在经过Self-attention层之后的x‘再加上原本的input，输出 $y = f (x) + x$ ,它用于解决梯度消失、梯度爆炸等问题。

再接着，对 Residual 作 Norm $\overset{x_{i}}{^} = \frac{x _{i} - m}{σ}$

Masked Self-attention

在Decoder当中，由于输出值是通过不断循环而推理出的，Self-attention不能在一开始就知道后面的token和自己的相关性，因此在这里是Masked的。

AutoRegressive

单看Decoder，其实它做着这样一件事：不断将output变成下一次的input，以这样类似于RNN的方式输出Seq。我们通过Begin token让Decoder知道从何时开始，而它通过输出End让我们知道在哪里结束，而Input持续不断的在Mask Muti-head Attention层影响Decoder。

Not AutoRegressive (NAT)

与AT不同的是，NAT并不会让Decoder循环输出，而是一次性完成，它设定一个输出的最大长度，然后每一个Token都使用Begin Token占位。它的好处在于并行与控制，在语音生成TTS中，NAT可以通过控制Token数量长度来控制语速。

How to decide the output length of NAT decoder?

Another Predictor from Encoder.
A maxium Length,ignore tokens after END token.

Performance: NAT < AT (because "Muti-modality")

Exposure bias

它是指一种现象：当Test的时候，Decoder一旦生成出局部错误内容会导致整体性的错误，这是因为Train数据的绝对正确。

Scheduled Sampling

针对Exposure bias，有目的的在Train中加入错误的数据，这被称为Scheduled Sampling。

FineTurning vs. Prompting

FineTurning	Prompting
专才	全才
通过Adapter	通过Prompting

各种Adapter

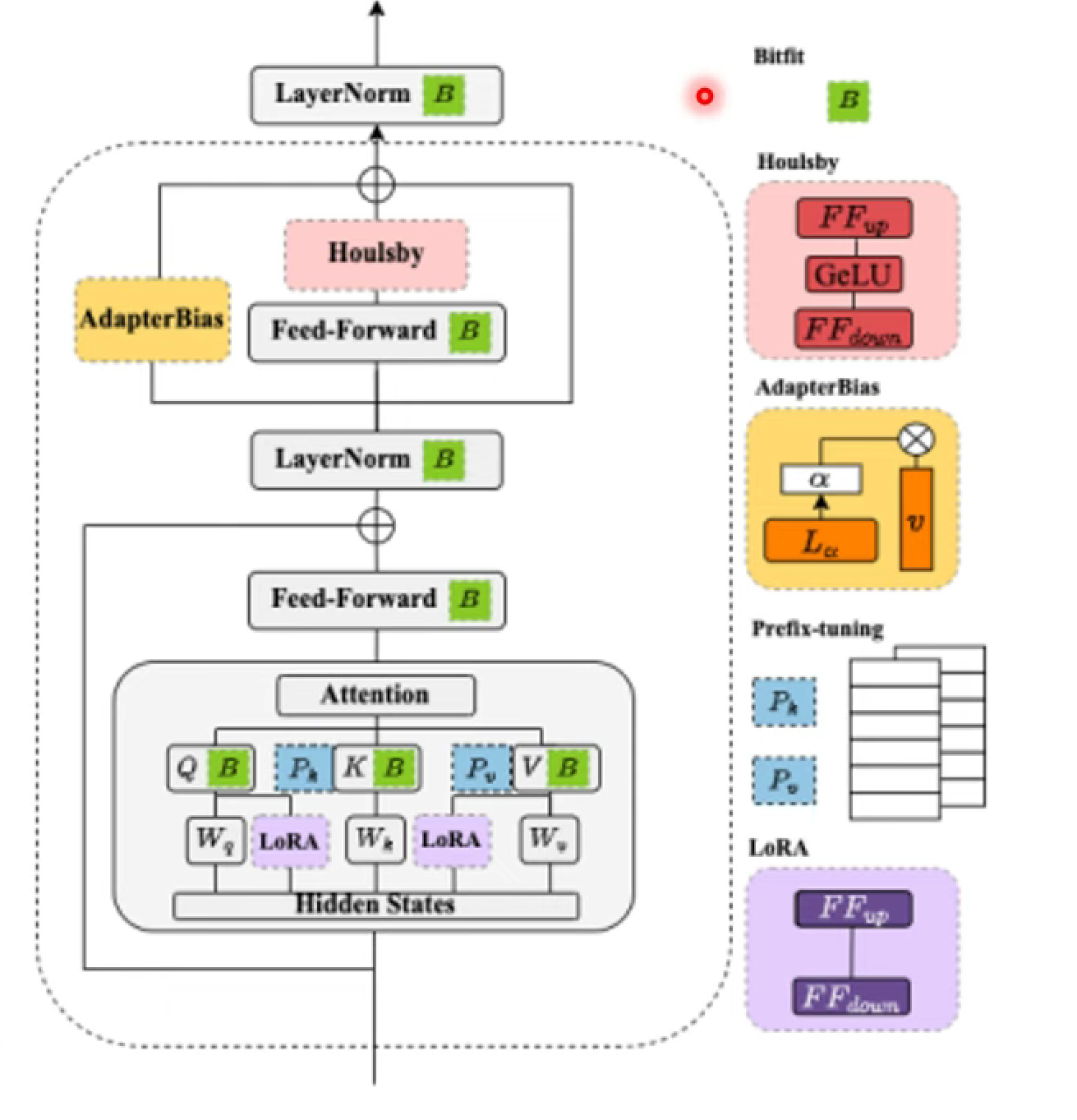
Bitfit：只微调Neural的bias
Houlsby：在Feed-Forward后面再插入一个Feed-Forward
adapter bias：与Feed-Forward平行，对Feed-Forward作平移等操作
Prefix/Lora：更改Attention参数

影像生成

现行的影像生成总是在Text $\to$ Image中加入一个从Normal Distribution里Sample出来的Vector，我的理解是这个Distribution是对真实图片的Distribution线性变换后产生的有限空间。

VAE：Vector来自于Encoder对Image的编码。
Flow-Base：Encoder与Decoder inverted，在通过Encoder对图像编码自然产生Vector。
diffusion model：将Vector视作真实噪音，仅通过add noise的方法生成Vector，将注意力放在denoise上。
GAN：再设计一个discriminator与decoder（genarate）进行对抗。

Denising Diffusion Probabilistic Model (DDPM)

Algorithm1 Training

repeat
$x_{0} \sim q (x_{0}) \leftarrow$ sampling clean image
$t \sim U ni f or m ({1, \dots, T})$
$ϵ \sim N (0, I) \leftarrow$ Sampling a noise
Take gradient desent step on: $\nabla_{θ} ∥ ϵ - ϵ_{θ} (\overline{α}_{t} x_{0} + 1 - \overline{α}_{t} ϵ, t) ∥^{2}$

与很多人想象的不同的是，DDPM在训练的时候，一次就将噪音加入Image中，并将它作为输入，让Denoise去预测生成的噪音。

Algorithm 2 Sample

$x_{T} \sim N (0, I)$
for $t = T, \dots, 1$ do
$z \sim N (0, I)$ if $t > 1$ ,else $z = 0$
$x_{t} - 1 = \frac{1}{α _{t}} (x_{t} - \frac{1 - α _{t}}{1 - α _{t}} ϵ_{θ} (x_{t}, t) + σ_{t} z)$
end if
return $x_{0}$

目前影像生成的目标

在一个已有的简单分布中，Sample一个z，在通过Denoise之后变成一张图片，这张图片实际上是在一个极其复杂的分布中。而影像生成的目标就是让这个分布与真实图片的分布越接近越好。